La validation des outils de mesure :

Pourquoi utiliser l’ACP dans la validation des échelles de mesure ?

En sciences de gestion, en marketing ou en sciences sociales, on cherche très souvent à mesurer des concepts abstraits : attitude, confiance, satisfaction, engagement, image de marque, etc. Ces concepts ne sont pas observables directement. On les approche donc à l’aide de plusieurs items (questions) censés mesurer différentes facettes d’un même construit.

L’Analyse en Composantes Principales (ACP) est un outil statistique fondamental qui permet de répondre à une question centrale :

👉 Les items mesurent-ils bien une ou plusieurs dimensions cohérentes ?

Autrement dit, l’ACP permet de :

• vérifier si les items se regroupent bien en facteurs cohérents,
• identifier le nombre de dimensions réelles sous-jacentes à une échelle,
• détecter les items mal positionnés, ambigus ou redondants,
• simplifier l’information en réduisant la dimension des données sans perdre trop d’information.

Dans une démarche de validation d’outil de mesure, l’ACP joue donc un rôle clé dans la validation de la structure interne de l’échelle.

---

À quoi sert concrètement l’ACP ?

L’ACP a trois objectifs principaux dans le cadre d’un questionnaire :

1. Vérifier la dimensionalité de l’échelle

Une échelle peut être :

• unidimensionnelle : tous les items mesurent le même concept,
• multidimensionnelle : les items se répartissent sur plusieurs dimensions (par exemple : confiance cognitive vs confiance affective).

L’ACP permet d’identifier empiriquement :

• combien de dimensions existent réellement dans les données,
• et quels items appartiennent à quelle dimension.

---

2. Vérifier que les items vont bien ensemble

Une bonne échelle doit présenter :

• des items fortement corrélés entre eux à l’intérieur d’une même dimension,
• et faiblement corrélés avec les autres dimensions.

L’ACP permet d’identifier :

• les items qui ne chargent sur aucun facteur,
• les items qui chargent sur plusieurs facteurs (items ambigus),
• les items qui ne contribuent pas réellement à la structure de l’échelle.

Ces items doivent en général être supprimés ou reformulés.

---

3. Réduire les données à des scores synthétiques

Une fois la structure validée, l’ACP permet de :

• construire des scores factoriels (ou scores de composantes),
• utiliser ces scores dans des analyses ultérieures (régressions, modèles structurels, comparaisons de groupes, etc.).

---

Conditions d’utilisation de l’ACP

Avant d’interpréter une ACP, il faut vérifier que les données s’y prêtent.

1. Le test KMO (Kaiser-Meyer-Olkin)

Le KMO mesure si les corrélations entre items sont suffisantes pour justifier une analyse factorielle.

• KMO < 0,5 : ❌ données inexploitables
• 0,5 – 0,6 : ⚠️ médiocre
• 0,6 – 0,7 : acceptable
• 0,7 – 0,8 : bon
• 0,8 : très bon

👉 En pratique, on exige au minimum 0,6, et idéalement > 0,7.

---

2. Le test de Bartlett

Le test de Bartlett vérifie si la matrice de corrélation est significativement différente d’une matrice identité.

• Si p-value < 0,05 → ✅ les corrélations sont suffisantes pour lancer une ACP
• Si p-value > 0,05 → ❌ les variables ne sont pas assez liées entre elles

---

Comment fonctionne l’ACP, conceptuellement ?

L’ACP consiste à :

• transformer les variables initiales (items) en nouvelles variables synthétiques appelées composantes,
• ces composantes sont non corrélées entre elles,
• la première composante explique le maximum de variance, la deuxième explique le maximum restant, etc.

Chaque composante est une combinaison linéaire des items.

---

Étape 1 : déterminer le nombre de composantes à retenir

Plusieurs critères existent, mais le plus utilisé est :

Le critère de Kaiser

On conserve les composantes dont la valeur propre (eigenvalue) est supérieure à 1.

On utilise aussi :

• le Scree Plot (graphique des valeurs propres) pour repérer le “coude”,
• et le pourcentage de variance expliquée cumulée (souvent on vise au moins 50–60 % en sciences sociales).

---

Étape 2 : interpréter les charges factorielles (loadings)

Les charges factorielles indiquent la corrélation entre chaque item et chaque composante.

En pratique :

• un item est considéré comme appartenant à une dimension si sa charge est :
  • > 0,5 (ou a minima > 0,4),
• un item qui charge fortement sur plusieurs dimensions pose un problème d’ambiguïté,
• un item qui ne charge fortement sur aucune dimension doit être supprimé.

---

Étape 3 : les communalités

La communalité d’un item indique :

la part de variance de l’item expliquée par les composantes retenues.

• Communalité faible (< 0,4) → item mal expliqué par la structure factorielle
• Communalité élevée → item pertinent et bien représenté

---

Le cercle des corrélations : un outil graphique essentiel

Le cercle des corrélations permet de visualiser :

• la position des items par rapport aux deux premières composantes,
• les proximités entre items,
• les oppositions entre dimensions.

Règles de lecture :

• plus un item est proche du cercle, mieux il est représenté,
• des items proches mesurent la même chose,
• des items opposés mesurent des concepts opposés,
• des items orthogonaux sont indépendants.

C’est un outil pédagogique et analytique extrêmement puissant.

---

Lien entre ACP et fiabilité (alpha de Cronbach)

Une ACP bien structurée doit être complétée par une analyse de fiabilité :

• Alpha de Cronbach global
• Alpha si item supprimé

En pratique :

• une dimension validée par ACP mais avec un alpha < 0,7 est statistiquement fragile,
• inversement, un bon alpha sans structure factorielle claire est théoriquement douteux.

Les deux approches sont complémentaires.

---

2. Mise en oeuvre de l’ACP

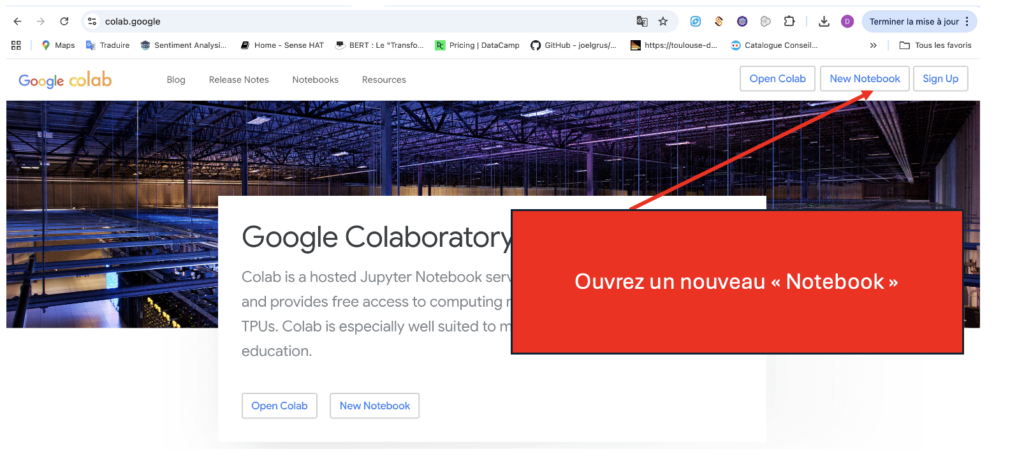
Cherchez Google colab sur Google et ouvrez un nouveau NoteBook :

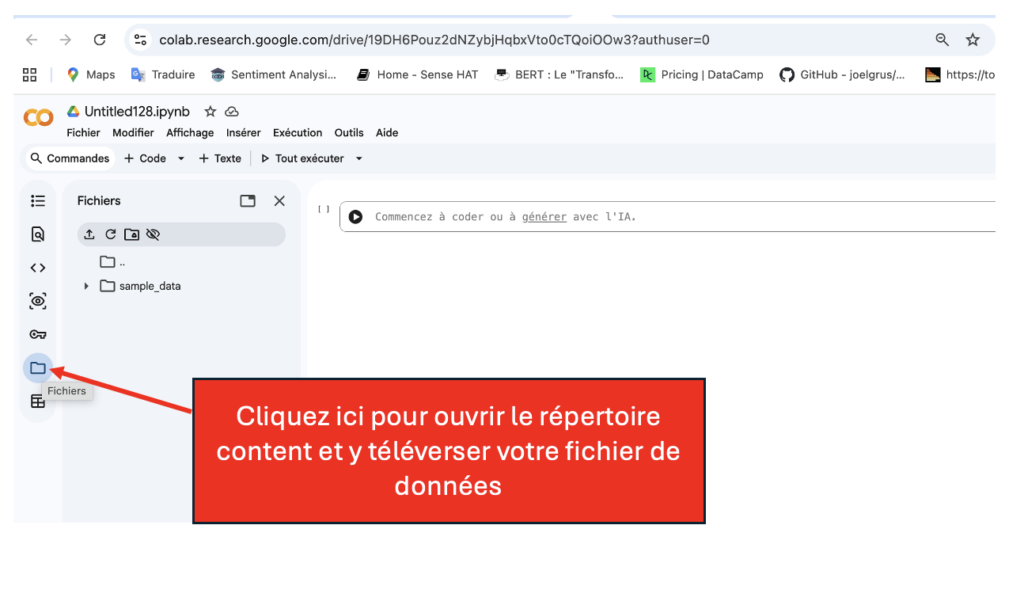
Les données test

Les trois fichiers à la fin de cette section contiennent les échelles de mesure pour quatre concepts centraux du modèle d’acceptation des robots humanoïdes :

• Confiance cognitive
• Confiance affective
• Attitude envers l’usage
• Intention d’usage

Chaque construit est mesuré par une échelle multi-items codée de façon identique dans les trois fichiers.

1. Confiance cognitive (CONFCO)

Objet mesuré : perception de la fiabilité et de la compétence du robot.

Code	Item
CONFCO1	Le robot semble fiable
CONFCO2	Je n’ai aucune raison de douter de sa compétence
CONFCO3	Je peux compter sur lui pour effectuer correctement sa tâche
CONFCO4	Les utilisateurs lui feront généralement confiance
CONFCO5	Il serait perçu comme digne de confiance par les autres

2. Confiance affective (CONFAFF)

Objet mesuré : sentiment de confort, de sécurité et de bienveillance dans l’interaction.

Code	Item
CONFAFF1	Si je comprenais mieux son fonctionnement, je m’inquiéterais davantage de ses performances
CONFAFF2	Je me sentirais à l’aise si ce robot interagissait avec moi
CONFAFF3	Le robot semble attentif à mon bien-être
CONFAFF4	Il réagirait de manière appropriée si je rencontrais une difficulté
CONFAFF5	Il me mettrait en confiance sur le plan émotionnel
CONFAFF6	Il me donnerait le sentiment d’être traité avec considération

3. Attitude envers l’usage (ATT)

Objet mesuré : évaluation globale, positive ou négative, de l’usage du robot.

Code	Item
ATT1	Utiliser ce robot serait une bonne idée
ATT2	L’usage de ce robot serait positif
ATT3	Je serais favorable à l’idée d’utiliser ce robot
ATT4	Utiliser ce robot serait bénéfique pour moi

4. Intention d’usage (INT)

Objet mesuré : disposition déclarée à utiliser réellement le robot.

Code	Item
INT1	J’ai l’intention d’accepter l’usage de ce robot
INT2	Je serais prêt(e) à l’utiliser si on me le proposait
INT3	Je l’utiliserais régulièrement s’il était disponible
INT4	Je recommanderais l’usage de ce robot

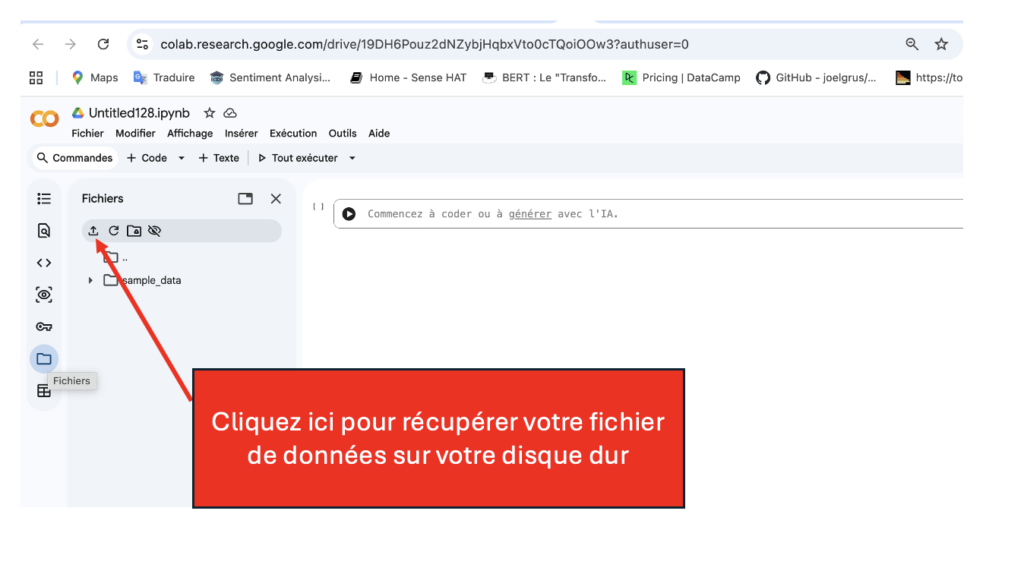
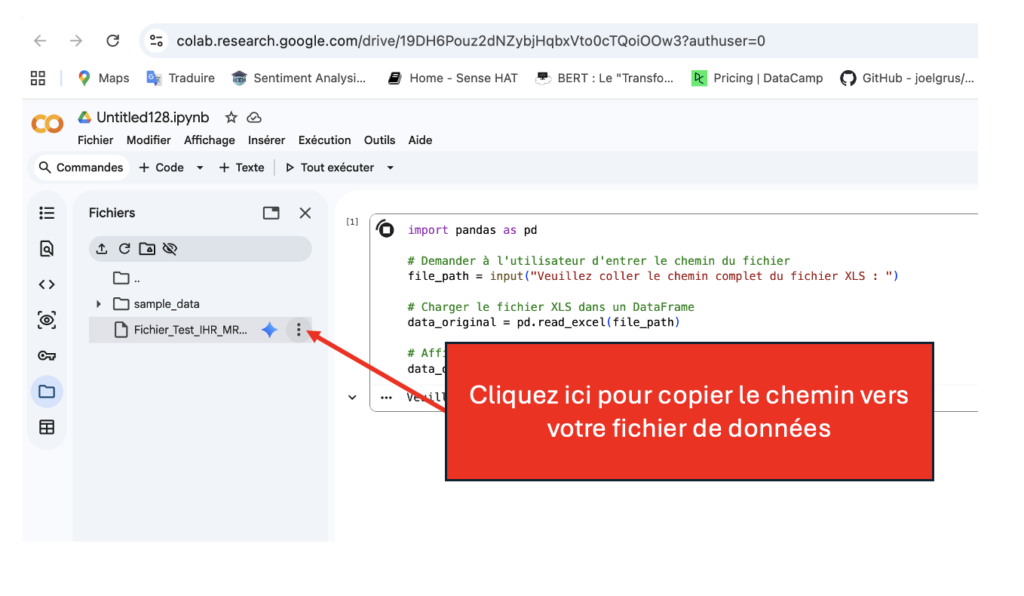
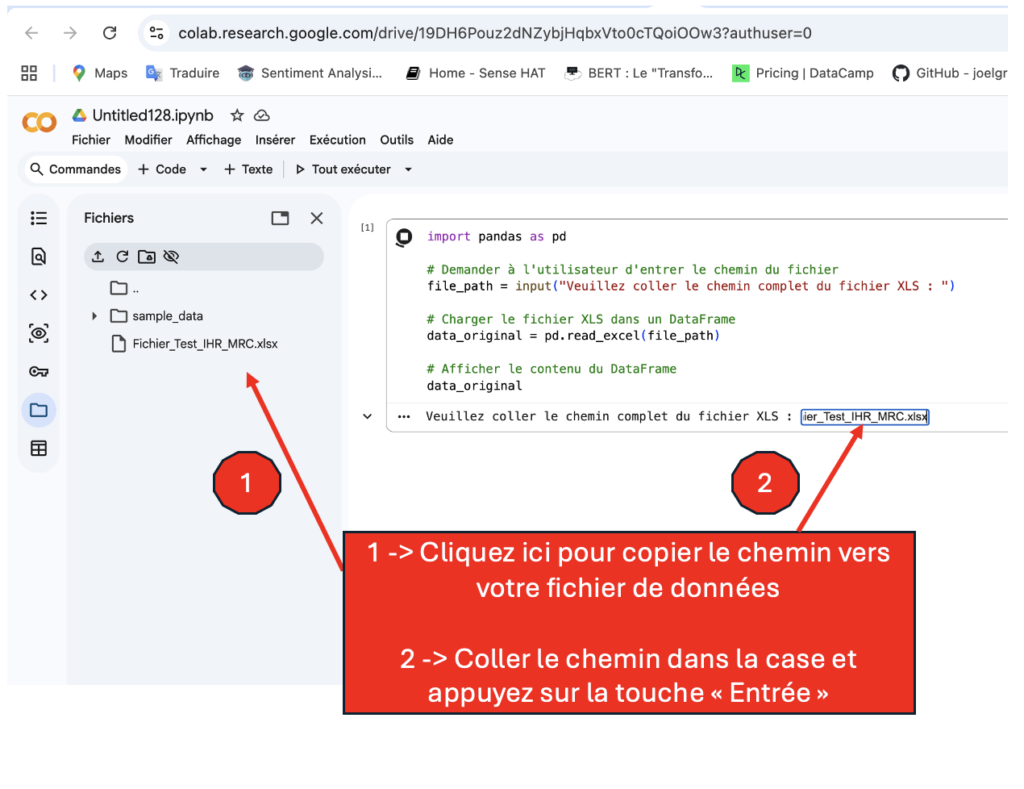
Cliquez sur “Ok” pour téléviser votre fichier de données :

Charger le fichier de données

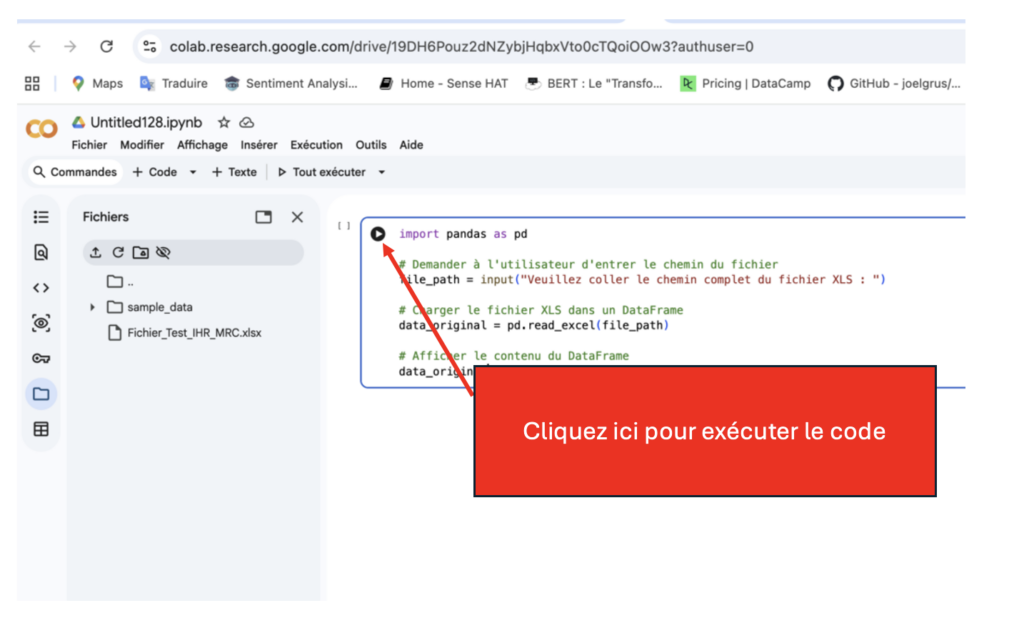
Copiez le code ci-dessous et collez-le sous Google Colab pour charger et afficher votre fichier de données :

import pandas as pd

# Demander à l'utilisateur d'entrer le chemin du fichier
file_path = input("Veuillez coller le chemin complet du fichier XLS : ")

# Charger le fichier XLS dans un DataFrame
data_original = pd.read_excel(file_path)

# Afficher le contenu du DataFrame
data_original

Installer les bibliothèques nécessaires

Copiez le code ci-dessous, collez-le dans la nouvelle cellule et exécutez-le : 

!pip install factor_analyzer
!pip install --upgrade scikit-learn
!pip install --upgrade --no-deps scikit-learn
!pip install --upgrade imbalanced-learn xgboost

Procéder à l’Analyse en Composantes Principales sans rotation

Copiez le code ci-dessous, collez-le dans la nouvelle cellule et exécutez-le : 

!pip install factor_analyzer
!pip install --upgrade scikit-learn
!pip install --upgrade --no-deps scikit-learn
!pip install --upgrade imbalanced-learn xgboost

Procéder à l’Analyse en Composantes Principales sans rotation

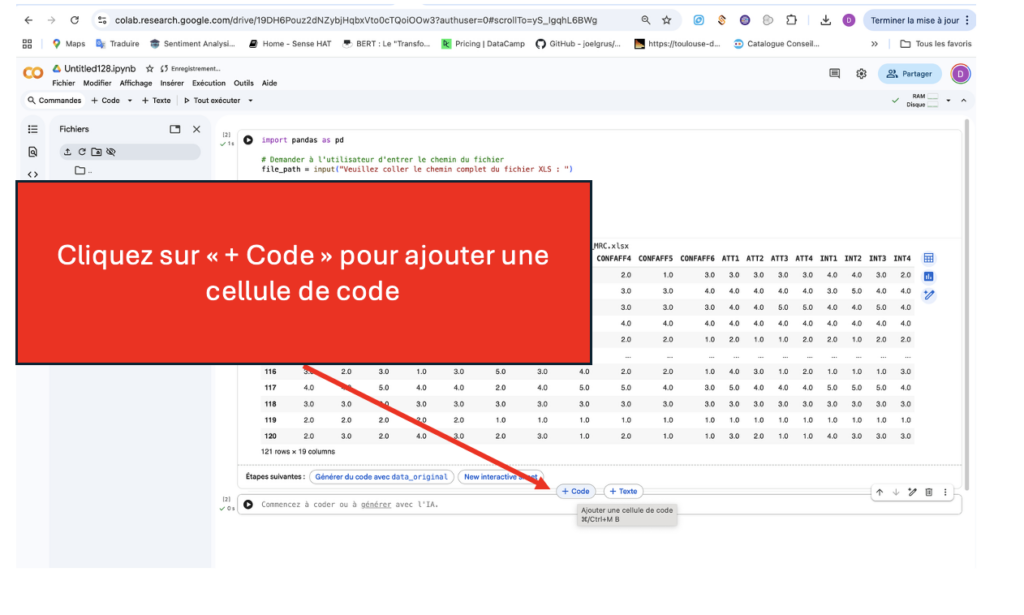
Ajoutez une cellule de code, copiez le code ci-dessous, collez-le dans la nouvelle cellule et exécutez-le.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from factor_analyzer.factor_analyzer import calculate_kmo, calculate_bartlett_sphericity
import ipywidgets as widgets
from IPython.display import display

# ============================================================
# UTILITAIRES
# ============================================================

def cronbach_alpha(df):
    if df.shape[1] > 1:
        k = df.shape[1]
        variances = df.var(axis=0, ddof=1)
        total_variance = df.sum(axis=1).var(ddof=1)
        return (k / (k - 1)) * (1 - (variances.sum() / total_variance))
    print("⚠️ Pas assez de variables pour calculer l'alpha sans item.")
    return np.nan

def select_columns(data):
    print("\nColonnes disponibles :", list(data.columns))
    selected_columns = input("Entrez les noms des colonnes pour l'ACP (séparées par une virgule) : ").strip().split(',')
    selected_columns = [col.strip() for col in selected_columns]
    if not all(col in data.columns for col in selected_columns):
        print("Erreur : certaines colonnes n'existent pas. Réessayez.")
        return select_columns(data)
    return selected_columns

def plot_correlation_circle(loadings, labels, title="Cercle des corrélations (F1-F2)"):
    if loadings.shape[1] < 2:
        print("ℹ️ Cercle des corrélations non affiché : il faut au moins 2 composantes.")
        return

    fig, ax = plt.subplots(figsize=(6, 6))
    ax.set_xlim(-1, 1)
    ax.set_ylim(-1, 1)

    # cercle unité
    theta = np.linspace(0, 2*np.pi, 400)
    ax.plot(np.cos(theta), np.sin(theta), linewidth=1)

    ax.axhline(0, color='black', linewidth=0.8)
    ax.axvline(0, color='black', linewidth=0.8)
    ax.grid(True, linestyle='--', linewidth=0.5, alpha=0.7)

    for i, lab in enumerate(labels):
        x, y = loadings[i, 0], loadings[i, 1]
        ax.scatter(x, y, alpha=0.6, s=50)
        ax.text(x, y, lab, fontsize=8, ha='center', va='center')

    ax.set_title(title, fontsize=10)
    ax.set_xlabel("Composante 1")
    ax.set_ylabel("Composante 2")
    plt.show()

def generate_pca_summary(df, n_factors, loadings, communalities, kmo_model, global_alpha, eigenvalues, explained_ratio):
    if n_factors == 1:
        summary_data = []
        for i, var in enumerate(df.columns):
            corr_item = 1.000 if i == 0 else round(np.corrcoef(df.iloc[:, 0], df.iloc[:, i])[0, 1], 3)
            summary_data.append([
                var,
                round(loadings[i, 0], 3),
                "-",
                round(communalities[i], 3),
                corr_item
            ])

        summary_data.append(["KMO", round(kmo_model, 3), "-", "-", "-"])
        summary_data.append(["α de l’échelle", round(global_alpha, 3), "-", "-", "-"])
        summary_data.append(["Valeur propre du facteur", round(float(eigenvalues[0]), 3), "-", "-", "-"])
        summary_data.append(["Variance expliquée", round(float(explained_ratio[0] * 100), 3), "-", "-", "-"])

        columns = ["Items", "Contributions factorielles", "α sans item", "Qualité Extraction", "Correl. Items"]
        return pd.DataFrame(summary_data, columns=columns)

    return None

# ============================================================
# ACP
# ============================================================

# Étape 1 : Sélection
selected_columns = select_columns(data_original)
df = data_original[selected_columns].copy()

# Nettoyage minimal (fortement conseillé)
df = df.apply(pd.to_numeric, errors="coerce").replace([np.inf, -np.inf], np.nan).dropna(axis=0, how="any")
zero_var_cols = df.columns[df.nunique(dropna=True) <= 1].tolist()
if zero_var_cols:
    print("⚠️ Colonnes supprimées (variance nulle) :", zero_var_cols)
    df = df.drop(columns=zero_var_cols)
if df.shape[1] < 2:
    raise ValueError("Pas assez de variables après nettoyage pour lancer une ACP.")

# Étape 2 : Standardisation
scaler = StandardScaler()
X = scaler.fit_transform(df)

# Étape 3 : KMO / Bartlett (sur données brutes df, pas sur X)
kmo_all, kmo_model = calculate_kmo(df)
chi_square_value, p_value = calculate_bartlett_sphericity(df)
print(f"\nKMO global : {kmo_model:.3f}")
print(f"Test de Bartlett : Chi² = {chi_square_value:.3f}, p = {p_value:.3f}")

# Étape 4-5 : PCA complète (toutes composantes) pour valeurs propres + variance
pca_full = PCA()
pca_full.fit(X)

eigenvalues = pca_full.explained_variance_
explained_ratio = pca_full.explained_variance_ratio_
cumulative_variance = np.cumsum(explained_ratio)

n_factors_auto = int(np.sum(eigenvalues > 1))
print(f"Nombre de composantes (Kaiser > 1) : {n_factors_auto}")

variance_table = pd.DataFrame({
    'Composante': [f"Composante {i+1}" for i in range(len(eigenvalues))],
    'Valeurs propres': eigenvalues,
    'Variance expliquée (%)': explained_ratio * 100,
    'Variance expliquée cumulée (%)': cumulative_variance * 100
}).round(3)
display(variance_table)

plt.figure(figsize=(8, 6))
plt.plot(range(1, len(eigenvalues) + 1), eigenvalues, marker='o')
plt.title("Graphique des valeurs propres (Scree Plot)")
plt.xlabel("Composantes")
plt.ylabel("Valeurs propres")
plt.grid(True)
plt.show()

# Étape 6 : Choix utilisateur
n_factors = int(input("Entrez le nombre de composantes à retenir pour les scores factoriels : "))

# Étape 7 : PCA retenue
pca = PCA(n_components=n_factors)
scores = pca.fit_transform(X)

# Loadings (corr variables-composantes) :
# loadings = components_.T * sqrt(eigenvalues)
loadings = pca.components_.T * np.sqrt(pca.explained_variance_)

components_matrix = pd.DataFrame(loadings, index=df.columns,
                                 columns=[f"Composante {i+1}" for i in range(n_factors)]).round(3)
display(components_matrix)

# Communalités (sur variables standardisées) = somme des loading^2 sur les composantes retenues
communalities = np.sum(loadings**2, axis=1)
communalities_df = pd.DataFrame({
    "Variable": df.columns,
    "Initial": [1.000]*len(df.columns),
    "Communalité": communalities
}).round(3)
print("\nCommunalités des variables:")
display(communalities_df)

# Étape 8 : Cercle des corrélations (F1-F2)
plot_correlation_circle(loadings, labels=df.columns)

# Étape 9 : Nommage des composantes + scores
component_names = []
for i in range(n_factors):
    component_names.append(input(f"Entrez le nom pour la composante {i+1} : "))

factor_scores_df = pd.DataFrame(scores, columns=component_names)
display(factor_scores_df)

# Étape 10 : Alpha de Cronbach + alpha sans item
global_alpha = cronbach_alpha(df)
print(f"Alpha de Cronbach global : {global_alpha:.3f}")

alpha_sans_item = {col: cronbach_alpha(df.drop(columns=[col])) for col in df.columns}
df_alpha = pd.DataFrame.from_dict(alpha_sans_item, orient='index', columns=['Alpha sans item']).round(3)
display(df_alpha)

# Étape 11 : Synthèse si 1 composante
pca_summary = generate_pca_summary(
    df=df,
    n_factors=n_factors,
    loadings=loadings,
    communalities=communalities,
    kmo_model=kmo_model,
    global_alpha=global_alpha,
    eigenvalues=eigenvalues,
    explained_ratio=explained_ratio
)
if pca_summary is not None:
    display(pca_summary)

# ============================================================
# SAUVEGARDE
# ============================================================

def save_results():
    global data_original
    data_original = pd.concat([data_original, factor_scores_df], axis=1)
    output_file = "Analyse_PCA_Resultats.xlsx"
    with pd.ExcelWriter(output_file) as writer:
        factor_scores_df.to_excel(writer, sheet_name="Scores", index=False)
        components_matrix.to_excel(writer, sheet_name="Loadings")
        communalities_df.to_excel(writer, sheet_name="Communalites", index=False)
        df_alpha.to_excel(writer, sheet_name="Alpha_Cronbach", index=True)
        variance_table.to_excel(writer, sheet_name="Variance")
        if pca_summary is not None:
            pca_summary.to_excel(writer, sheet_name="Synthese_PCA_1D", index=False)
    print(f"\nLes résultats ont été sauvegardés dans {output_file}.")

save_btn = widgets.Button(description="Enregistrer les résultats")
save_btn.on_click(lambda b: save_results())
display(save_btn)

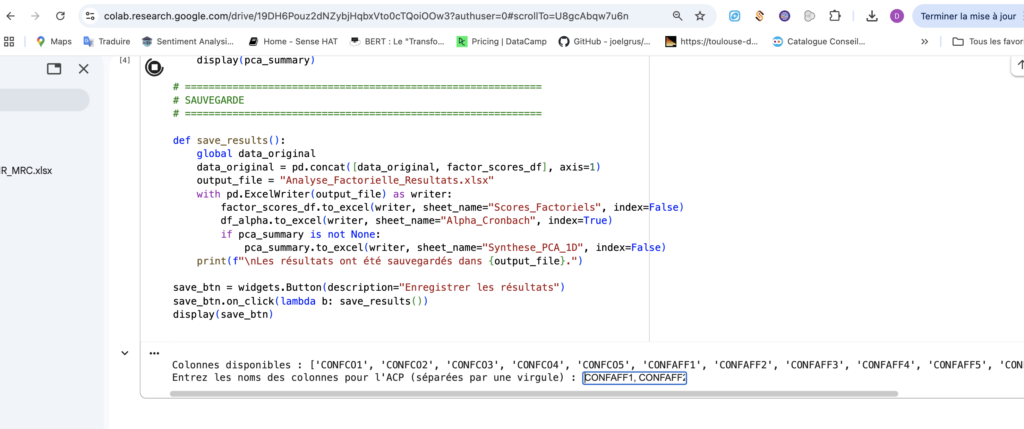
Voici un exemple avec la mesure de la confiance affective :

Attention à bien enlever les guillemets ‘ lorsque vous saisissez les noms des colonnes pour l’ACP.

Pensez à enregistrer les résultats.

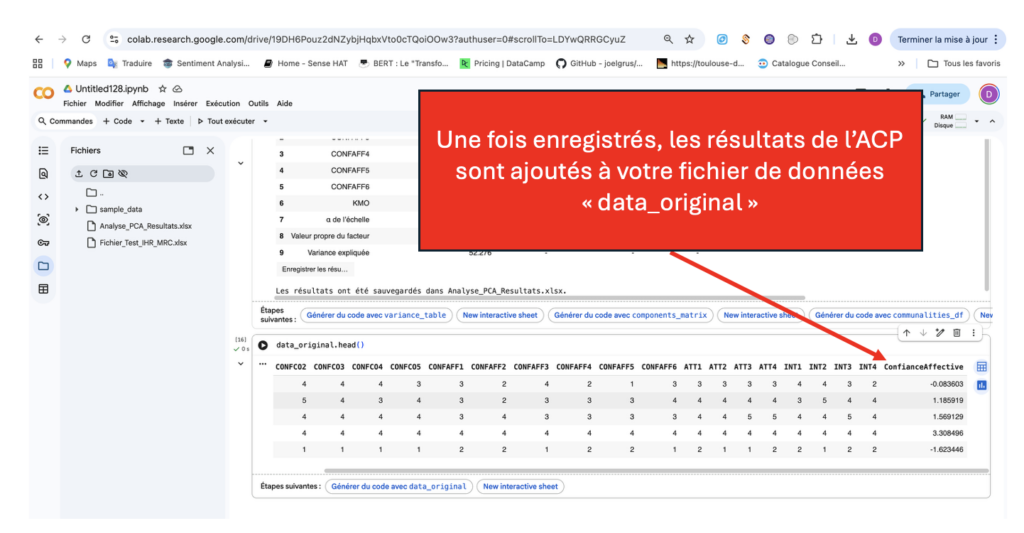
Un bout de code pour sauvegarder votre fichier contenant les scores factoriels des ACP réalisées

data_original.to_excel('data_original.xlsx', index=False)

# Télécharger le fichier Excel automatiquement sur votre ordinateur (spécifique à Google Colab)
from google.colab import files
files.download('data_original.xlsx')

Une fois toutes les échelles de mesure validées et les résultats des ACP enregistrés, vous pouvez passer au test du modèle …