Objectif de la page
Un modèle statistique n’a de valeur que si l’on vérifie qu’il tient la route : qualité d’ajustement, cohérence des relations estimées, absence de biais majeurs, et diagnostics minimaux (multicolinéarité, résidus, etc.). Ici, l’idée est de proposer un workflow simple et robuste pour tester un modèle (souvent une régression multiple) et produire un résultat exploitable dans un mémoire ou un article.
Ce que vous trouverez ici
- Les tests indispensables (et à quoi ils servent)
- Un code Python réutilisable
- Une grille d’interprétation rapide
- Des remarques de bon sens (ce que le modèle ne dit pas)
Après avoir réalisé toutes vos ACP et obtenu vos scores, vous pouvez mettre en œuvre le test de votre modèle via une régression multiple, puis vérifier la normalité des résidus, l’hétéroscédasticité et la multicolinéarité (VIF).
Avant de lancer la régression : vérifiez que les scores de vos ACP sont bien enregistrés dans
data_original.

Code Python (régression multiple + diagnostics)
Attention à saisir les noms de vos variables telles quelles sont dans vos données data_original.
import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler
from statsmodels.stats.outliers_influence import variance_inflation_factor
# Sélectionner les variables explicatives (X) et la variable dépendante (y)
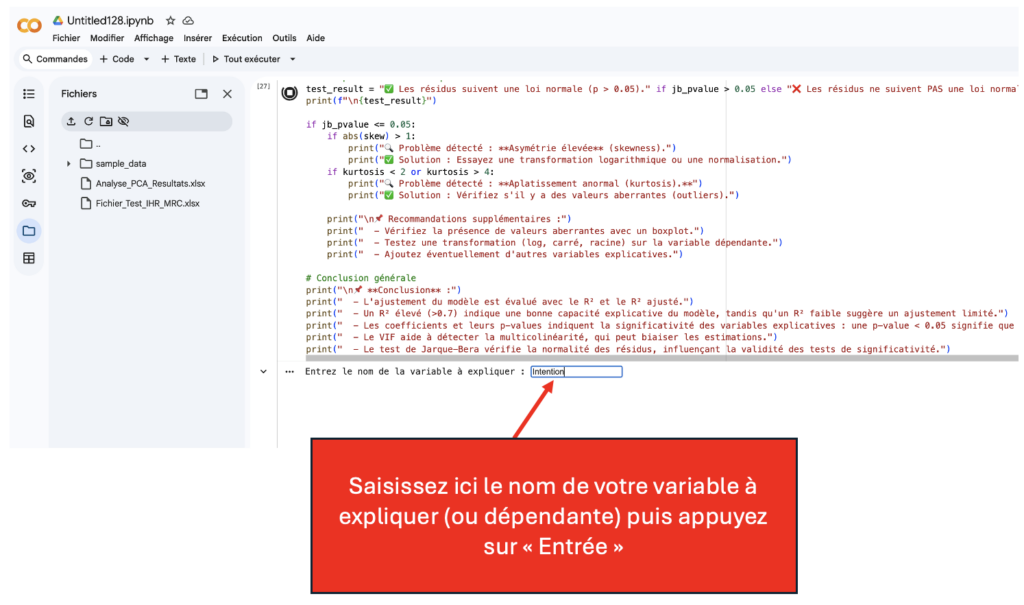
y_var = input("Entrez le nom de la variable dépendante : ").strip()
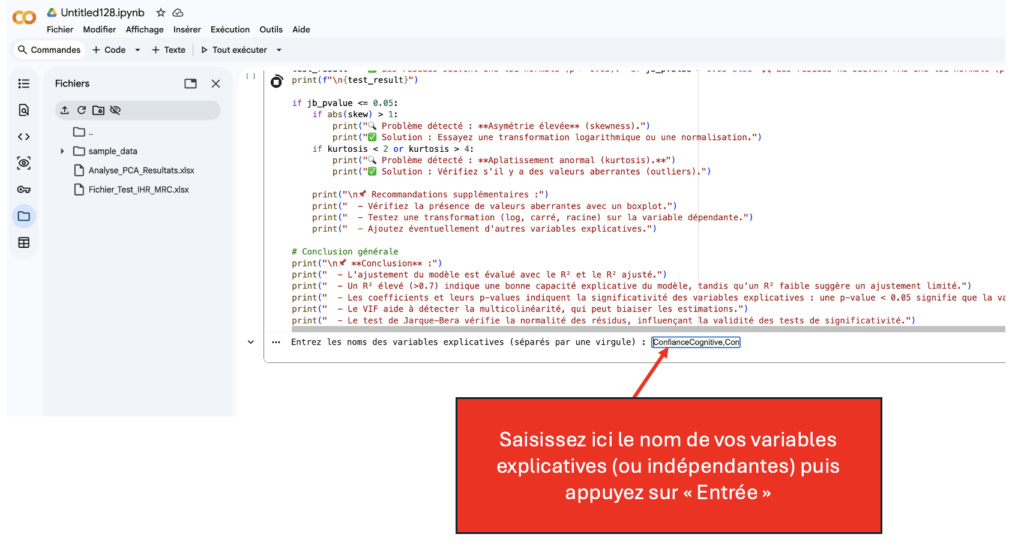
X_vars = input("Entrez les noms des variables explicatives (séparés par une virgule) : ").strip().split(",")
# Vérification des variables
if y_var not in data_original.columns or any(var not in data_original.columns for var in X_vars):
raise ValueError("Erreur : Assurez-vous que toutes les variables existent dans le DataFrame.")
# Définir X et y
X = data_original[X_vars] # Suppression de l'ajout de la constante
y = data_original[y_var]
# Vérifier si X contient au moins une variable
if X.shape[1] == 0:
raise ValueError("Erreur : Aucune variable explicative valide sélectionnée.")
# Ajustement du modèle OLS
model = sm.OLS(y, X).fit()
print(model.summary())
# Vérification de la normalité des résidus avec un QQ-plot
residuals = model.resid
fig, ax = plt.subplots(figsize=(6, 6))
sm.qqplot(residuals, line="s", ax=ax)
ax.set_title("QQ-Plot des résidus")
plt.show()
# Vérification de l'hétéroscédasticité avec un scatter plot
plt.figure(figsize=(8, 5))
sns.scatterplot(x=model.fittedvalues, y=residuals)
plt.axhline(0, linestyle="dashed", color="red")
plt.xlabel("Valeurs ajustées")
plt.ylabel("Résidus")
plt.title("Graphique des résidus")
plt.show()
# Calcul du VIF pour détecter la multicolinéarité
if X.shape[1] > 1: # Vérifier que le VIF peut être calculé
vif_data = pd.DataFrame({
"Variable": X.columns,
"VIF": [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
})
print("\n Facteur d'inflation de la variance (VIF) :")
display(vif_data)
# Interprétation du VIF
high_vif = vif_data[vif_data["VIF"] > 10]
if not high_vif.empty:
print("\n⚠️ Attention : Certaines variables présentent une forte multicolinéarité (VIF > 10). Cela peut affecter la fiabilité des coefficients estimés.")
print(high_vif)
else:
print("✅ Aucune multicolinéarité préoccupante détectée (VIF < 10).")
else:
print("\n⚠️ Pas assez de variables pour calculer le VIF.")
# Test de normalité des résidus (Jarque-Bera)
jb_stat, jb_pvalue, skew, kurtosis = sm.stats.jarque_bera(residuals)
print("\n Résultats du Test de normalité de Jarque-Bera :")
print(f" - Statistique JB : {jb_stat:.3f}")
print(f" - p-value : {jb_pvalue:.5f}")
print(f" - Asymétrie (Skewness) : {skew:.3f}")
print(f" - Aplatissement (Kurtosis) : {kurtosis:.3f}")
# Interprétation automatique
test_result = "✅ Les résidus suivent une loi normale (p > 0.05)." if jb_pvalue > 0.05 else "❌ Les résidus ne suivent PAS une loi normale (p ≤ 0.05)."
print(f"\n{test_result}")
if jb_pvalue <= 0.05:
if abs(skew) > 1:
print(" Problème détecté : **Asymétrie élevée** (skewness).")
print("✅ Solution : Essayez une transformation logarithmique ou une normalisation.")
if kurtosis < 2 or kurtosis > 4:
print(" Problème détecté : **Aplatissement anormal (kurtosis).**")
print("✅ Solution : Vérifiez s'il y a des valeurs aberrantes (outliers).")
print("\n Recommandations supplémentaires :")
print(" - Vérifiez la présence de valeurs aberrantes avec un boxplot.")
print(" - Testez une transformation (log, carré, racine) sur la variable dépendante.")
print(" - Ajoutez éventuellement d'autres variables explicatives.")
# Conclusion générale
print("\n **Conclusion** :")
print(" - L'ajustement du modèle est évalué avec le R² et le R² ajusté.")
print(" - Un R² élevé (>0.7) indique une bonne capacité explicative du modèle, tandis qu'un R² faible suggère un ajustement limité.")
print(" - Les coefficients et leurs p-values indiquent la significativité des variables explicatives : une p-value < 0.05 signifie que la variable a un impact significatif.")
print(" - Le VIF aide à détecter la multicolinéarité, qui peut biaiser les estimations.")
print(" - Le test de Jarque-Bera vérifie la normalité des résidus, influençant la validité des tests de significativité.")📌 Lecture et limites : repères rapides
Comment lire les résultats
- R² / R² ajusté : part de variance expliquée (comparaison entre modèles).
- Coefficients : direction et intensité de l’effet (signe + amplitude).
- p-value / IC : solidité statistique (attention à la taille d’échantillon).
- VIF : si trop élevé, vos coefficients deviennent peu interprétables.
Ce que le modèle ne dit pas
- Corrélation ≠ causalité (sauf dispositif causal / expérimental).
- Un “bon” R² ne garantit pas une bonne mesure des construits.
- Un résultat significatif peut être trivial en pratique (effet minuscule).
- Si l’échantillon est biaisé, le modèle peut être “bon” mais inutile.
🧪 Les diagnostics à faire (simple, efficace)
| Diagnostic | Pourquoi | Règle pratique | Action si problème |
|---|---|---|---|
| Multicolinéarité (VIF) | Évite des coefficients instables et des erreurs d’interprétation | VIF élevé = variables trop redondantes | Retirer/agréger variables, re-spécifier le modèle |
| Résidus (normalité / forme) | Vérifie que les hypothèses de base ne sont pas catastrophiques | Regarder QQ-plot, histo, patterns | Transformer variables, robust SE, re-modéliser |
| Qualité d’ajustement | Mesure ce que le modèle explique réellement | R² / R² ajusté + taille d’effet | Ajouter variables pertinentes, revoir mesure |
| Significativité / cohérence | Confirme ou invalide les hypothèses | Coefficients + p-values + IC | Re-spécifier, tester modérations/mediations, vérifier items |
Remarque : les “seuils” ne sont pas des lois de la nature. Le but est d’éviter les erreurs grossières et de documenter vos choix.